Welcome to baccoemu’s documentation!
baccoemu is a collection of cosmological neural-network emulators for large-scale structure statistics. Specifically, we provide fast predictions for:
the linear cold- and total-matter power spectrum (paper, tutorial)
the modifications to the cold-matter power spectrum caused by baryonic physics (paper, tutorial)
the power spectrum of biased tracers in real space in the context of the hybrid Lagrangian bias expansion (paper, tutorial)
in a wide cosmological parameter space, including dynamical dark energy and massive neutrinos. These emulators were developed as part of the Bacco project – for more details, visit our main website.
Our emulators are publicly available under MIT licence; please, follow the links above to be see te corresponding papers on the arXiv website, where you can find all the references to credit our work.
Note
The bacco project is under constant development and new versions of the emulators become available as we improve them. Follow our public repository to make sure you are always up to date with our latest release.
Installation
As a quick summary, you shouldn’t need anything more than
pip install baccoemu [--user]
You can also install the development version from bitbucket by cloning and installing the source
git clone https://bitbucket.org/rangulo/baccoemu.git
cd baccoemu
pip install . [--user]
You can then test that the installation was successful:
python -m unittest test.test_baccoemu
It should take a couple of seconds and not return any errors.
Warning
the bacco emulator only works in a
Python 3 environment; the data file at its core cannot
be unpickled by Python 2.x; in case your pip
command doesn’t link to a Python 3 pip executable, please
modify the line above accordingly (e.g. with pip3 instead of pip)
Note
The bacco emulator depends on some external packages, namely
numpy
scikit-learn
keras
tensorflow
matplotlib
scipy
progressbar2
The installation process will automatically try to install them if they are not already present.
Loading and emulator info
There are two emulator classes, one for the matter power spectrum emulator (linear and nonlinear), and one for the power spectrum of biased tracers in real space. They can be loaded with
import baccoemu
mpk_emulator = baccoemu.Matter_powerspectrum()
lbias_emulator = baccoemu.Lbias_expansion()
Each emulator object holds some very useful information. For example, focusing on th elinear emulator, to know the k-range on which the emulator is defined you can type
import baccoemu
mpk_emulator = baccoemu.Matter_powerspectrum()
print(mpk_emulator.emulator['linear']['k'])
Similarly, to know the free parameters on which the linear emulator is defined and which is the allowed range of each of them, you can type
for key, bound in zip(mpk_emulator.emulator['linear']['keys'], mpk_emulator.emulator['linear']['bounds']):
print(key, bound)
By changing linear to nonlinear, you can find this kind of information for the nonlinear emulator.
The same thing applies to the biased tracers power spectrum emulator, for example
import baccoemu
lbias_emulator = baccoemu.Lbias_expansion()
print(lbias_emulator.emulator['nonlinear']['k'])
Tutorial linear emulators
Let’s assume you want to evaluate the linear power spectra emulators at a given set of wavemodes and for a given cosmology and redshift. First, you should load baccoemu (and define your wavemodes vector)
import baccoemu
emulator = baccoemu.Matter_powerspectrum()
import numpy as np
k = np.logspace(-2, np.log10(5), num=100)
All the bacco emulators take as an input a set of cosmological parameters. This can be passed as a dictionary, like
params = {
'omega_cold' : 0.315,
'sigma8_cold' : 0.83, # if A_s is not specified
'omega_baryon' : 0.05,
'ns' : 0.96,
'hubble' : 0.67,
'neutrino_mass' : 0.0,
'w0' : -1.0,
'wa' : 0.0,
'expfactor' : 1
}
Please note that omega_cold and sigma8_cold refer to the density parameter and linear variance of cold matter (cdm + baryons), which does not correspond to the total matter content in massive neutrino cosmologies. Also note that A_s can be specified instead of sigma8_cold, but be aware these parameters are mutually exclusive.
You can evaluate the linear matter power spectrum emulator (for cold matter and total matter) via
k, pk_lin_cold = emulator.get_linear_pk(k=k, cold=True, **params)
k, pk_lin_total = emulator.get_linear_pk(k=k, cold=False, **params)
Tutorial nonlinear emulators
Let’s assume you want to evaluate the nonlinear power spectra emulators at a given set of wavemodes and for a given cosmology and redshift. First, you should load baccoemu (and define your wavemodes vector)
import baccoemu
emulator = baccoemu.Matter_powerspectrum()
import numpy as np
k = np.logspace(-2, np.log10(emulator.emulator['nonlinear']['k'].max()), num=100)
All the bacco emulators take as an input a set of cosmological parameters. This can be passed as a dictionary, like
params = {
'omega_cold' : 0.315,
'sigma8_cold' : 0.83, # if A_s is not specified
'omega_baryon' : 0.05,
'ns' : 0.96,
'hubble' : 0.67,
'neutrino_mass' : 0.0,
'w0' : -1.0,
'wa' : 0.0,
'expfactor' : 1
}
Please note that omega_cold and sigma8_cold refer to the density parameter and linear variance of cold matter (cdm + baryons), which does not correspond to the total matter content in massive neutrino cosmologies. Also note that A_s can be specified instead of sigma8_cold, but be aware these parameters are mutually exclusive.
You can evaluate the nonlinear boost and the nonlinear matter power spectrum emulator (for cold matter and total matter) via
k, Q_cold = emulator.get_nonlinear_boost(k=k, cold=True, **params)
k, Q_total = emulator.get_nonlinear_boost(k=k, cold=False, **params)
k, pk_nl_cold = emulator.get_nonlinear_pk(k=k, cold=True, **params)
k, pk_nl_total = emulator.get_nonlinear_pk(k=k, cold=False, **params)
These are the nonlinear boost Q (which, multiplied by the corresponding linear power spectrum gives the nonlinear power spectrum), the emulated linear power spectrum pk and the emulated nonlinear power spectrum pknl. We can have a look at them
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1,2, figsize=(10,5))
ax[0].loglog(k, Q_cold)
ax[1].loglog(k, pk_lin, label="Linear Power Spectrum")
ax[1].loglog(k, pk_nl_cold, label="Nonlinear Power Spectrum")
ax[0].set_xlabel("k [h/Mpc]"); ax[1].set_xlabel("k [h/Mpc]");
ax[0].set_ylabel("Q"); ax[1].set_ylabel("P(k)");
plt.legend()
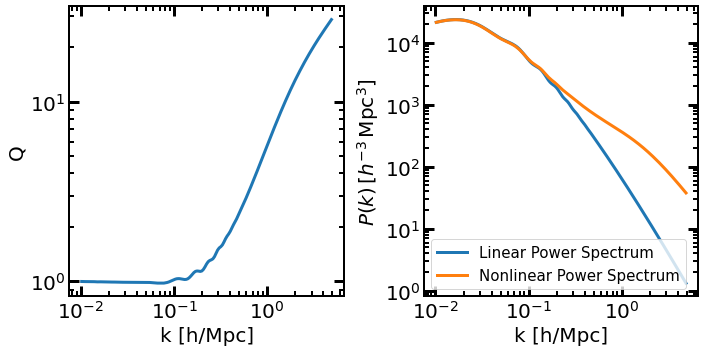
Note that to get the nonlinear power spectrum, baccoemu will internally multiply the boost factor Q by the emulated linear power spectrum. If you want to use another linear power spectrum, you can pass it via
k, pknl = emulator.get_nonlinear_pk(params, k=k, baryonic_boost=False, k_lin=your_k, pk_lin=your_linear_pk)
Tutorial baryon-corrected power spectrum emulator
First, you should load baccoemu (and define your wavemodes vector)
import baccoemu
emulator = baccoemu.Matter_powerspectrum()
import numpy as np
k = np.logspace(-2, np.log10(emulator.emulator['nonlinear']['k'].max()), num=100)
When baryonic corrections are required, the parameter dictionary must include the relevant parameters, such as
params = {
'omega_cold' : 0.315,
'sigma8_cold' : 0.83,
'omega_baryon' : 0.05,
'ns' : 0.96,
'hubble' : 0.67,
'neutrino_mass' : 0.0,
'w0' : -1.0,
'wa' : 0.0,
'expfactor' : 1,
'M_c' : 14,
'eta' : -0.3,
'beta' : -0.22,
'M1_z0_cen' : 10.5,
'theta_out' : 0.25,
'theta_inn' : -0.86,
'M_inn' : 13.4
}
In this case, the baryonic boost is obtained through
k, S = emulator.get_baryonic_boost(k=k, **params)
which is defined as the ratio between the power spectrum under the effect of baryons to that considering only gravitational forces. Finally, the nonlinear matter power spectrum with baryonic effects can be obtained with
k, pknl = emulator.get_nonlinear_pk(k=k, baryonic_boost=True, **params)
We can display them both:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1,2, figsize=(10,5))
ax[0].semilogx(ks, S)
ax[1].loglog(knl, pk, label="Linear P(k)")
ax[1].loglog(knl, pknl, label="Nonlinear P(k)")
ax[1].loglog(knl, pknl_b, label="Nonlinear P(k) & Baryons")
ax[0].set_xlabel("k [h/Mpc]"); ax[1].set_xlabel("k [h/Mpc]");
ax[0].set_ylabel(r"$S=P_{\rm baryons}/P_{\rm gravity\,only}$"); ax[1].set_ylabel("$P(k)\,[h^{-3}\,\mathrm{Mpc}^{3}]$");
plt.legend()
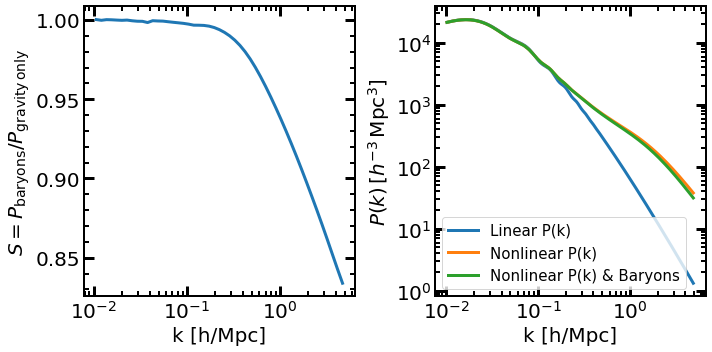
Tutorial biased tracers in real space
The biased tracers power spectrum emulator is loaded with (including accessing to its k vector)
import baccoemu
emulator = baccoemu.Lbias_expansion()
import numpy as np
k = np.logspace(-2, np.log10(emulator.emulator['nonlinear']['k'].max()), num=100)
The cosmological parameters are specified in the same way as for the other emulators
params = {
'omega_cold' : 0.315,
'sigma8_cold' : 0.83, # if A_s is not specified
'omega_baryon' : 0.05,
'ns' : 0.96,
'hubble' : 0.67,
'neutrino_mass' : 0.0,
'w0' : -1.0,
'wa' : 0.0,
'expfactor' : 1
}
In this case we can obtain the 15 terms needed for reconstructing the biased tracers power spectrum with
k, pnn = emulator.get_nonlinear_pnn(k=k, **params)
Here pnn is a list of 15 power spectra (each of length len(k)) corresponding to the terms \(11\), \(1\delta\), \(1\delta^2\), \(1s^2\), \(1\nabla^2\delta\), \(\delta \delta\), \(\delta \delta^2\), \(\delta s^2\), \(\delta \nabla^2\delta\), \(\delta^2 \delta^2\), \(\delta^2 s^2\), \(\delta^2 \nabla^2\delta\), \(s^2 s^2\), \(s^2 \nabla^2\delta\), \(\nabla^2\delta \nabla^2\delta\).
Alternatevely, instead of manually combining these terms, one can get the galaxy-galaxy and galaxy-matter power spectra by specifying the bias parameters and using the following method
bias_params = [0.75, 0.25, 0.1, 1.4] # b1, b2, bs2, blaplacian
k, p_gg, p_gm = emulator.get_galaxy_real_pk(bias=bias_params, k=k, **params)
Note that this does not include any stocastic noise, so the user shoud add it manually to the p_gg vector.
Vectorized usage
You can evaluate the baccoemu emulators at many coordinates at the same time. For the vectorized version of baccoemu, you can vary one or more parameters at the same time.
In the first case, you will have to define the parameters as
import baccoemu
emulator = baccoemu.Matter_powerspectrum()
import numpy as np
k = np.logspace(-2, np.log10(5), num=100)
params = {
'omega_cold' : 0.315,
'sigma8_cold' : 0.83, # if A_s is not specified
'omega_baryon' : 0.05,
'ns' : 0.96,
'hubble' : 0.67,
'neutrino_mass' : 0.0,
'w0' : -1.0,
'wa' : 0.0,
'expfactor' : np.linspace(0.5, 1, 10)
}
k, pk_i = emulator.get_nonlinear_pk(k=k, **params)
In the second case you will have to pass you parameters like
import numpy as np
k = np.logspace(-2, np.log10(5), num=100)
import baccoemu
emulator = baccoemu.Matter_powerspectrum()
params = {
'omega_cold' : [ 0.315, 0.27],
'sigma8_cold' : [ 0.83, 0.83],
'omega_baryon' : [ 0.05, 0.04],
'ns' : [ 0.96, 0.98],
'hubble' : [ 0.67, 0.73],
'neutrino_mass' : 0.0,
'w0' : -1.0,
'wa' : 0.0,
'expfactor' : [ 0.5, 1.0]
}
k, pk_i = emulator.get_nonlinear_pk(k=k, **params)
Note that not all the parameters have to be varied (you can keep one or more fixed), but the ones that are varied must have the same array length.
The vectorised usage is available for all of our emulators, linear and nonlinear power spectrum, and biased tracers power spectra.
Parameter space
The parameters used for the different emulators must be enclosed within the following boundaries
linear cold and total matter spectrum emulator
|
0.15 |
0.6 |
\(\Omega_{cb} = \Omega_{cdm} + \Omega_{b}\) (cdm+baryons) |
|
0.03 |
0.07 |
\(\Omega_{b}\) |
|
any |
any |
\(A_s\) |
|
any |
any |
\(\sigma_{8,cb}\) (cdm+baryons) |
|
any |
any |
\(n_s\) |
|
0.5 |
0.9 |
\(h = H_0/100\) |
|
0 |
0.5 |
\(M_\nu = \sum m_{\nu,i} [\mathrm{eV}]\) |
|
-1.3 |
-0.7 |
\(w_0\) |
|
-0.5 |
0.5 |
\(w_a\) |
|
0.25 |
1 |
\(a = 1 / (1 + z)\) |
\(k \in [10^{-4}, 50]\,\, h \,\, \mathrm{Mpc}^{-1}\)
nonlinear matter power spectrum emulator
|
0.23 |
0.4 |
\(\Omega_{cb} = \Omega_{cdm} + \Omega_{b}\) (cdm+baryons) |
|
0.04 |
0.06 |
\(\Omega_{b}\) |
|
0.73 |
0.9 |
\(\sigma_{8,cb}\) (cdm+baryons) |
|
0.92 |
1.01 |
\(n_s\) |
|
0.6 |
0.8 |
\(h = H_0/100\) |
|
0 |
0.4 |
\(M_\nu = \sum m_{\nu,i} [\mathrm{eV}]\) |
|
-1.15 |
-0.85 |
\(w_0\) |
|
-0.3 |
0.3 |
\(w_a\) |
|
0.4 |
1 |
\(a = 1 / (1 + z)\) |
\(k \in [10^{-2}, 5] \,\, h \,\, \mathrm{Mpc}^{-1}\)
baryonic boost emulator
|
9 |
15 |
\(\log_{10}[M_{\rm c} / (M_\odot/h)]\) |
|
-0.69 |
0.69 |
\(\log_{10}[\eta]\) |
|
-1 |
0.69 |
\(\log_{10}[\beta]\) |
|
9 |
13 |
\(\log_{10}[M_{z_0,\mathrm{cen}} / (M_\odot/h)]\) |
|
0 |
0.47 |
\(\log_{10}[\vartheta_{\rm out}]\) |
|
-2 |
-0.52 |
\(\log_{10}[\vartheta_{\rm inn}]\) |
|
9 |
13.5 |
\(\log_{10}[M_{\rm inn} / (M_\odot/h)]\) |
\(k \in [10^{-2}, 5] \,\, h \,\, \mathrm{Mpc}^{-1}\)
biased tracers real space power spectrum emulator
|
0.23 |
0.4 |
\(\Omega_{cb} = \Omega_{cdm} + \Omega_{b}\) (cdm+baryons) |
|
0.04 |
0.06 |
\(\Omega_{b}\) |
|
0.73 |
0.9 |
\(\sigma_{8,cb}\) (cdm+baryons) |
|
0.92 |
1.01 |
\(n_s\) |
|
0.6 |
0.8 |
\(h = H_0/100\) |
|
0 |
0.4 |
\(M_\nu = \sum m_{\nu,i} [\mathrm{eV}]\) |
|
-1.15 |
-0.85 |
\(w_0\) |
|
-0.3 |
0.3 |
\(w_a\) |
|
0.4 |
1 |
\(a = 1 / (1 + z)\) |
\(k \in [10^{-2}, 0.71] \,\, h \,\, \mathrm{Mpc}^{-1}\)
Complete API
- class baccoemu.Matter_powerspectrum(*args: Any, **kwargs: Any)
- class baccoemu.Matter_powerspectrum(linear=True, smeared_bao=False, no_wiggles=True, nonlinear_boost=True, baryonic_boost=True, compute_sigma8=True, nonlinear_emu_path=None, nonlinear_emu_details=None, baryonic_emu_path=None, baryonic_emu_details=None, verbose=True)
A class to load and call the baccoemu for the matter powerspectrum. By default, the linear power spectrum (described in Aricò et al. 2021), the nonlinear boost (described in Angulo et al. 2020), and the baryonic boost (described in Aricò et al. 2020c) are loaded.
The emulators for A_s, sigma8, sigma12, and the smearing and removing of the BAO are also available.
At large scales, i.e. k<0.01, the ratios between non-linear/linear and baryonic/non-linear spectra is considered to be 1.
- Parameters:
linear (boolean, optional) – whether to load the linear emulator, defaults to True
smeared_bao (boolean, optional) – whether to load the smeared-BAO emulator, defaults to False
no_wiggles (boolean, optional) – whether to load the no-wiggles emulator, defaults to True
nonlinear_boost (boolean, optional) – whether to load the nonlinear boost emulator, defaults to True
baryonic_boost (boolean, optional) – whether to load the baryonic boost emulator, defaults to True
compute_sigma8 (boolean, optional) – whether to load the sigma8 emulator, defaults to True
verbose (boolean, optional) – whether to activate the verbose mode, defaults to True
- get_A_s(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, **kwargs)
Return A_s, corresponding to a given sigma8_cold at a set of coordinates in parameter space.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
- Returns:
A_s
- Return type:
float or array
- get_baryonic_boost(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, M_c=None, eta=None, beta=None, M1_z0_cen=None, theta_out=None, theta_inn=None, M_inn=None, k=None, **kwargs)
Evaluate the baryonic emulator at a set of coordinates in parameter space.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
M_c (float or array) – mass fraction of hot gas in haloes
eta (float or array) – extent of ejected gas
beta (float or array) – mass fraction of hot gas in haloes
M1_z0_cen (float or array) – characteristic halo mass scale for central galaxy
theta_out (float or array) – density profile of hot gas in haloes
theta_inn (float or array) – density profile of hot gas in haloes
M_inn (float or array) – density profile of hot gas in haloes
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the baryonic emulator will be used, defaults to None
grid (array_like, optional) – dictionary with parameter and vector of values where to evaluate the emulator, defaults to None
- Returns:
k and S(k), the emulated baryonic boost of P(k)
- Return type:
tuple
- get_linear_pk(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, cold=True, **kwargs)
Evaluate the linear emulator at a set of coordinates in parameter space.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the linear emulator will be used, defaults to None
k_lin (array_like, optional) – a vector of wavemodes in h/Mpc, if None the wavemodes used by the linear emulator are returned, defaults to None
pk_lin (array_like, optional) – a vector of linear power spectrum computed at k_lin, if None the linear emulator will be called, defaults to None
cold (bool, optional) – whether to return the cold matter power spectrum or the total one. Default to cold.
- Returns:
k and the linear P(k)
- Return type:
tuple
- get_no_wiggles_pk(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, k_lin=None, pk_lin=None, **kwargs)
Evaluate the cold matter power spectrum with no wiggles (no bao), calling an emulator at a set of coordinates in parameter space.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_coldor omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the linear emulator will be used, defaults to None
k_lin (array_like, optional) – a vector of wavemodes in h/Mpc, if None the wavemodes used by the linear emulator are returned, defaults to None
pk_lin (array_like, optional) – a vector of linear power spectrum computed at k_lin, if None the linear emulator will be called, defaults to None
grid (array_like, optional) – dictionary with parameters and vectors of values where to evaluate the emulator, defaults to None
- Returns:
k and the linear P(k)
- Return type:
tuple
- get_nonlinear_boost(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, k_lin=None, pk_lin=None, cold=True, **kwargs)
Compute the prediction of the nonlinear boost of cold matter power spectrum
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the nonlinear emulator will be used, defaults to None
k_lin (array_like, optional) – a vector of wavemodes in h/Mpc, if None the wavemodes used by the linear emulator are returned, defaults to None
pk_lin (array_like, optional) – a vector of linear power spectrum computed at k_lin, if None the linear emulator will be called, defaults to None
cold (bool, optional) – whether to return the cold matter power spectrum or the total one. Default to cold.
- Returns:
k and Q(k), the emulated nonlinear boost of P(k)
- Return type:
tuple
- get_nonlinear_pk(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, M_c=None, eta=None, beta=None, M1_z0_cen=None, theta_out=None, theta_inn=None, M_inn=None, k=None, k_lin=None, pk_lin=None, cold=True, baryonic_boost=False, **kwargs)
Compute the prediction of the nonlinear cold matter power spectrum.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
M_c (float or array) – mass fraction of hot gas in haloes
eta (float or array) – extent of ejected gas
beta (float or array) – mass fraction of hot gas in haloes
M1_z0_cen (float or array) – characteristic halo mass scale for central galaxy
theta_out (float or array) – density profile of hot gas in haloes
theta_inn (float or array) – density profile of hot gas in haloes
M_inn (float or array) – density profile of hot gas in haloes
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the emulator will be used, defaults to None
k_lin (array_like, optional) – a vector of wavemodes in h/Mpc, if None the wavemodes used by the linear emulator are returned, defaults to None
pk_lin (array_like, optional) – a vector of linear power spectrum computed at k_lin, if None the linear emulator will be called, defaults to None
cold (bool, optional) – whether to return the cold matter power spectrum or the total one. Default to cold.
- Returns:
k and the nonlinear P(k)
- Return type:
tuple
- get_sigma12(cold=True, omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, **kwargs)
Return sigma12, calling an emulator at a set of coordinates in parameter space.
- Parameters:
cold (bool) – whether to return sigma8_cold (cdm+baryons) or total matter
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
- Returns:
sigma12
- Return type:
float or array
- get_sigma8(cold=True, omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, **kwargs)
- Return sigma8, calling an emulator
at a set of coordinates in parameter space.
- Parameters:
cold (bool) – whether to return sigma8_cold (cdm+baryons) or total matter
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
- Returns:
sigma8
- Return type:
float or array
- get_smeared_bao_pk(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Evaluate the cold matter power spectrum with smeared bao, calling an emulator at a set of coordinates in parameter space.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the linear emulator will be used, defaults to None
k_lin (array_like, optional) – a vector of wavemodes in h/Mpc, if None the wavemodes used by the linear emulator are returned, defaults to None
pk_lin (array_like, optional) – a vector of linear power spectrum computed at k_lin, if None the linear emulator will be called, defaults to None
grid (array_like, optional) – dictionary with parameters and vectors of values where to evaluate the emulator, defaults to None
- Returns:
k and the linear P(k)
- Return type:
tuple
- baccoemu.matter_powerspectrum.compute_camb_pk(coordinates, k=None, cold=True)
Compute the linear prediction of the matter power spectrum using camb
The coordinates must be specified as a dictionary with the following keywords:
‘omega_cold’
‘omega_baryon’
‘sigma8’
‘hubble’
‘ns’
‘neutrino_mass’
‘w0’
‘wa’
‘expfactor’
- Parameters:
coordinates (dict) – a set of coordinates in parameter space
k (array_like, optional) – a vector of wavemodes in h/Mpc, if None the wavemodes used by camb are returned, defaults to None
cold (bool, optional) – whether to return the cold matter power spectrum or the total one. Default to cold.
- Returns:
k and linear pk
- Return type:
tuple
- baccoemu.baryonic_boost.get_baryon_fractions(M_200c, omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, M_c=None, eta=None, beta=None, M1_z0_cen=None, theta_out=None, theta_inn=None, M_inn=None)
Compute the mass fraction of the different baryonic components, following the baryonic correction model described in Aricò et al 2020b (see also Aricò et al 2020a).
- Parameters:
M_200 (array_like) – Halo mass inside a sphere which encompass a density 200 times larger than the critical density of the Universe.
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
M_c (float or array) – mass fraction of hot gas in haloes
eta (float or array) – extent of ejected gas
beta (float or array) – mass fraction of hot gas in haloes
M1_z0_cen (float or array) – characteristic halo mass scale for central galaxy
theta_out (float or array) – density profile of hot gas in haloes
theta_inn (float or array) – density profile of hot gas in haloes
M_inn (float or array) – density profile of hot gas in haloes
- Returns:
a dictionary containing the baryonic components mass fractions, with the following keywords:
‘ej_gas’ -> ejected gas
‘cen_galaxy’ -> central galaxy
‘sat_galaxy’ -> satellite galaxy
‘bo_gas’ -> bound gas
‘re_gas’ -> reaccreted gas
‘dark_matter’ -> dark matter
‘gas’ -> total gas
‘stellar’ -> total stars
‘baryon’ -> total baryons
- Return type:
dict
- class baccoemu.Lbias_expansion(lpt=True, smeared_bao=True, nonlinear_boost=True, compute_sigma8=True, verbose=True)
A class to load and call baccoemu for the Lagrangian bias expansion terms. By default, the nonlinear Lagrangian bias expansion terms emulator (described in Zennaro et al, 2021) and LPT lagrangian bias expansion terms emulator (described in Aricò et al, 2021) are loaded. Another emulator loaded by deafult is the IR-resummed linear power spectrum.
- Parameters:
lpt (boolean, optional) – whether to load the LPT emulator, defaults to True
compute_sigma8 (boolean, optional) – whether to load the sigma8 emulator, defaults to True
smeared_bao (boolean, optional) – whether to load the smeared bao, defaults to True
nonlinear_boost (boolean, optional) – whether to load the nonlinear boost emulator, defaults to True
compute_sigma8 – whether to load the sigma8 emulator, defaults to True
verbose (boolean, optional) – whether to activate the verbose mode, defaults to True
- Hubble(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Hubble function in km / s / Mpc
Warning: neutrino and dynamical dark energy not yet implemented Warning: no radiation included
- comoving_radial_distance(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Comoving radial distance in Mpc/h
Warning: neutrino and dynamical dark energy not yet implemented Warning: no radiation included
- get_galaxy_real_pk(bias=None, omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Compute the predicted galaxy auto pk and galaxy-matter cross pk given a set of bias parameters
- Parameters:
bias (array-like) – a list of bias parameters, including b1, b2, bs2, blaplacian
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the nonlinear emulator will be used, defaults to None
- Returns:
k and P(k), a list of the emulated 15 LPT Lagrangian bias expansion terms
- Return type:
tuple
- get_lpt_pk(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Compute the prediction of the 15 LPT Lagrangian bias expansion terms.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the nonlinear emulator will be used, defaults to None
- Returns:
k and P(k), a list of the emulated 15 LPT Lagrangian bias expansion terms
- Return type:
tuple
- get_nonlinear_pnn(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Compute the prediction of the nonlinear cold matter power spectrum.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the nonlinear emulator will be used, defaults to None
- Returns:
k and P(k), a list of the emulated 15 LPT Lagrangian bias expansion terms
- Return type:
tuple
- get_smeared_bao_pk(omega_cold=None, omega_matter=None, omega_baryon=None, sigma8_cold=None, A_s=None, hubble=None, ns=None, neutrino_mass=None, w0=None, wa=None, expfactor=None, k=None, **kwargs)
Evaluate the smeared bao emulator at a set of coordinates in parameter space.
- Parameters:
omega_cold (float or array) – omega cold matter (cdm + baryons), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
omega_matter (float or array) – omega total matter (cdm + baryons + neutrinos), either omega_cold or omega_matter should be specified, if both are specified they should be consistent
sigma8_cold (float or array) – rms of cold (cdm + baryons) linear perturbations, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
A_s (float or array) – primordial scalar amplitude at k=0.05 1/Mpc, either sigma8_cold or A_s should be specified, if both are specified they should be consistent
hubble (float or array) – adimensional Hubble parameters, h=H0/(100 km/s/Mpc)
ns (float or array) – scalar spectral index
neutrino_mass (float or array) – total neutrino mass
w0 (float or array) – dark energy equation of state redshift 0 parameter
wa (float or array) – dark energy equation of state redshift dependent parameter
expfactor (float or array) – expansion factor a = 1 / (1 + z)
k (array_like, optional) – a vector of wavemodes in h/Mpc at which the nonlinear boost will be computed, if None the default wavemodes of the nonlinear emulator will be used, defaults to None
- Returns:
k and P(k), a list of the emulated 15 LPT Lagrangian bias expansion terms
- Return type:
tuple